Blog 5: Hypothesis Testing
- Matthias Ng
- Feb 4, 2023
- 2 min read
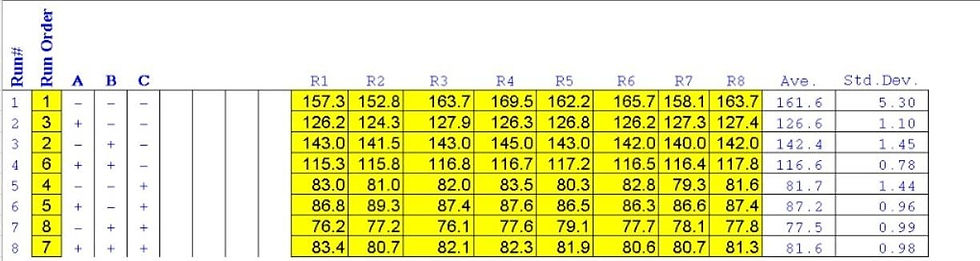
To determine the effect of projectile weight on the flying distance of the projectile
Scope of the Test:
The human effect is assumed to be negligible. Therefore, different user will not have any effect on the flying distance of the projectile
Flying distance for catapult is collected using the factors below:
Arm length = ____ cm
Projectile weight = _____ grams and ______ grams
Stop angle = _____ degree
State the null hypothesis (H0):
Using the lighter projectile (Run #1) and the heavier projectile (Run #3) will result in the same distance travelled by the projectile.
𝜇₁ = 𝜇₃
State the alternative hypothesis (H1):
Using the lighter projectile (Run #1) would lead to it having a further distance travelled when compared to the heavier projectile (Run #3) .
𝜇₁ > 𝜇₃
Sample size is 16 Therefore t-test will be used.
Since the sign of H1 is > , a ̶l̶e̶f̶t̶/̶t̶w̶o̶/right tailed test is used.
Significance level (α) used in this test is 0.05
State the mean and standard deviation of Run #1 (lighter projectile):
Mean: 161.6cm
Standard deviation: 5.3cm
State the mean and standard deviation of Run #3(heavier projectile):
Mean: 142.5cm
Standard deviation: 1.45cm
Compute the value of the test statistic (t):
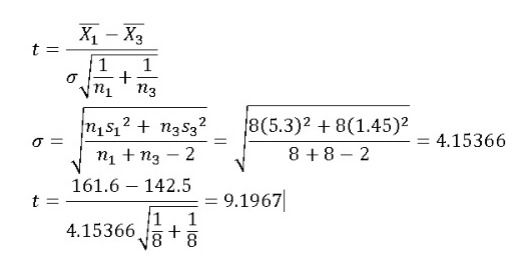
Type of test (check one only)
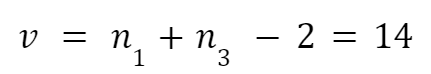
1.Left-tailed test: [ __ ] Critical value tα= - ______
2.Right-tailed test:[ ✔️ ] Critical value tα= 1.761
3.Two-tailed test:[ __ ] Critical value tα/2= ± ______
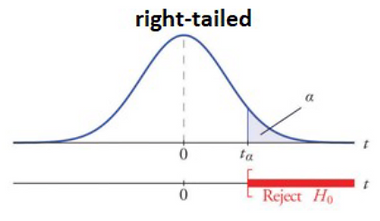
Compare the values of test statistics, t, and critical value(s),tα or ±̶t̶α̶/̶2̶
Therefore Ho is false.
Conclusion that answers the initial question: Using a lighter projectile leads to the projectile flying a larger distance while using a heavier projectile leads to the projectile flying a shorter distance.
Compare your conclusion from other team members:
What inferences can you make from these comparisons:
Learning Reflection
During the CPDD lesson on hypothesis, I found it difficult to understand the topic and how to carry out hypothesis testing


Comments